Last updated on March 1, 2013
Nuclear reactors contain tons of fissile material and nuclear bombs contain only kilograms of fissile materials, so why does one of them explode with enough force to flatten a city but the other doesn’t? I will pull out some latex skillz and geek it out with equations to describe the physics behind whats in nuclear engineering is called reactivity excursions or RIA (Reactivity Insertion Accident). The level of these blog posts will be such that an interested and fairly math savy person can understand and calculate these kind of things on their own.
Castle Romeo photo: United States Department of Energy, Source: Wikimedia
There is more things going on in a nuclear reactor than only nuclear reactions, the nuclear reactions produce heat, the heat is transferred through the fuel into the coolant (in most cases water). When water is heated things happen like changes in pressure, changes in phase (in other words the water can start boiling) etc. These changes in the water properties then goes on to influence the nuclear reactions. If density goes down moderation of neutrons gets less efficient, if water starts boiling it cools the fuel less efficiently and the temperature of the fuel influence the nuclear reactions within the fuel through a processes called doppler resonance broadening. One ends up with a quite complicated situation where all kinds of different physical processes interact with each other in feedback loops (nuclear engineers where early pioneers in what is now hyped and called “multiphysics”, where several branches of physics interact). Luckily, as always with physics, one can make a whole bunch of approximations and end up with a situation that is fairly simple and intuitive but still accurate enough to be worthwhile to study. I will go through it all step by step.
The nuclear side of things
Any nuclear engineer or reactor physicist worth his salt can be awoke in the middle of the night, given pen and paper, and be able to fluently write out the neutron diffusion equation. The diffusion equation is the bread and butter of nuclear engineering. Sure the transport equation is its mom and monte carlo simulations might be more sexy but the diffusion equation is the main work horse. To brush up one some basic terms I recommend that you read this blog post before reading this part.
Castle Romeo photo: Teuni Source: Wikimedia. License: Creative Commons Attribution-Share Alike 3.0 unported
The diffusion equation can be derived from the transport equation or simply found by reasoning, but we will not go into that this time, if you are curious you can have a look in this book. It can be written as:
$$\Large D\nabla^{2}\phi – \Sigma_{a}\phi + S =\frac{1}{v}\frac{d\phi}{dt} $$
The neutron diffusion equation simply describes a neutron balance and each term in the equation represents one physical process that changes the balance. Each term is:
$$\Large\frac{d\phi}{dt} $$, $$\large\phi$$ is the neutron flux, it tells you how many neutrons pass through a surface in a second (the unit is neutrons/$$cm^2s$$) and $$\large d\phi/dt$$ is the change of neutron flux in time. $$\large\nabla^{2}\phi$$ represents the leakage of neutrons out of the system.
$$\Large\nabla^2$$ is the Laplace operator. $$\large\Sigma_{a}\phi\large$$ tells you how many neutrons get lost by absorbtion in the material, $$\large\Sigma_{a}$$ is the absorption cross section and $$\large\phi$$ is the neutron flux, the flux times the cross section gives the nuclear reaction rate. The subscript a stands for absorption.
$$\Large S$$ is simply a source of neutrons, if there is fissile material in the system then this is the term that describes how many neutrons are produced from fission. Basically what the equation say is that the change in neutron flux in a system over time is equal to the leakage of neutrons minus the absorption of neutrons plus the production of neutrons. It’s like counting apples in a truck, change in the number of apples is equal to apples added to the truck minus apples eaten by worms minus apples falling of the truck.
Lets start to simplify this, first lets assume we have a infinite reactor of homogeneous material. This is equivalent to saying:
$$\Large \nabla^2\phi=0$$
I.e no matter where in the system you are everything looks alike. Now we are left with the source term and absorption term. The source term is simple, if you read the blog post I linked to then you remember that if you put a bunch of neutrons in a system with fissile material the neutrons will bounces around, gets absorbed and some of them will split an atom and produces new neutrons. The number of neutrons in the next “neutron generation” will be equal to the initial number of neutrons times the multiplication factor, $$\large K_{\infty}$$. The source term will be equal to number of neutrons absorbed in the material times the multiplication factor:
$$\Large S=K_{\infty}\Sigma_{a}\phi$$.
There is a detail here however that we need to introduce, it turns out that when you split a nuclide you get radioactive decay products. Some of these decay products throw out a neutron when decaying, that means these decays are another source of neutrons. Usually one say that a fraction of the neutrons, $$\large\beta$$ is born out of decays, these neutrons are called delayed neutrons because there is a time delay between the fission product being born until it decays. The neutrons produced right away by fission is called prompt neutrons. If we take this into account the source term we get is:
$$\Large S=(1-\beta)K_{\infty}\Sigma_{a}\phi+\sum_{i}\lambda_{i}C_{i}$$
$$\Large \sum_{i}\lambda_{i}C_{i}$$ is just good old basic nuclear decay term, C is the concentration of fission products that decay by producing neutrons and $$\large\lambda$$ is the decay constant. The subscript i signifies that the fission products that decay and produces neutrons can be lumped into i number of groups, each with a decay constant. To make things a bit tidy we will also introduce two other quantity. First the prompt neutron lifetime, it will be denoted by the symbol $$\large\Lambda$$. The prompt neutron lifetime is just what it sounds like, the time it takes between a prompt neutron being born and being absorbed somewhere. It can be shown that it is equal to:
$$\Large\Lambda = \frac{1}{\Sigma_{a}v}$$
where v is neutron velocity. Second we introduce the reactivity, it is defines as:
$$\Large\rho = \frac{K_{\infty}-1}{K_{\infty}}$$
Reactivity tells you how far away from criticality the system is. You can “insert” reactivity to a reactor by for instance manipulating control rods, changing boron level in the water, adding fresh fuel and so on.
Putting all of this into the neutron diffusion equation and massaging it a bit we end up with this tidy equation:
$$\Large\frac{d\phi}{dt} = \frac{\rho-\beta}{\Lambda}K_{\infty}\phi+v\sum_{i}\lambda_{i}C_{i}$$
This is called the point kinetics equation and it is an approximation of the time dependence of the neutron flux. The neutron flux happens to be directly proportional to the power so it also describes the time dependence of the power in a reactor. To make this complete we also need an equation for $$\large C_{i}$$. The concentration depends on the production of fission products and the decay of those same products.
$$\Large\frac{dC_{i}}{dt}=\beta_{i}K_{\infty}\Sigma_{a}\phi-\lambda_{i}C_{i}$$
This is the precursor equation. Notice that the precursor equation depends on the flux and the flux depends on the precursor equation. To get rid of the pesky neutron velocity, v, that shows up in the point kinetics equation we can note that $$\large\phi = vn$$ where n is neutron density (neutrons per cubic centimeter). If we replace $$\large\phi$$ with $$\large vn$$ everywhere we get these two equations instead.
$$\Large\frac{dn}{dt}=\frac{\rho-\beta}{\Lambda}K_{\infty}n+\sum_{i}\lambda_{i}C_{i}$$
$$\Large\frac{dC_{i}}{dt}=\frac{\beta_{i}K_{\infty}}{\Lambda}n-\lambda_{i}C_{i}$$
There are many different methods to solve this sucker, runge-kutta, forwards and backwards Euler method and so on. The above equations also have an analytical solution if one assumes that $$\large\rho$$ and $$\large K_{\infty}$$ are not functions of time. Later in this blog post series we want to look specifically at situations where $$\large\rho$$ is not constant and thus the analytical solutions are of little value, but I will spend some time on them anyway because the analytic solutions are always educational.
No delayed neutrons
Lets look at the simplest solution, if we have no delayed neutrons, i.e $$\large\beta=0$$, then the precursor equation disappears and we are left with:
$$\Large\frac{dn}{dt}=\frac{k_{\infty}-1}{\Lambda}\phi$$
That equation has the trivial solution:
$$\Large\phi(t) = constant*e^{\frac{k_{\infty}-1}{\Lambda}t}$$
We can easily calculate the doubling time (time for power to double), it is:
$$\Large T = \frac{0.693*\Lambda}{k_{\infty}-1}$$
$$\Lambda$$ usually has a value around 200 microseconds in a thermal reactor. In such a reactor, if $$\large K_{\infty}$$ deviates from 1 with as little as one part in a thousand (less than the value of a single control rod) the power will double every 0.14 seconds! It will increase by well over a hundred times in just one second. A nuclear weapon is far worse, it has a shorter neutron lifetime of about $$\large 10^{-7}$$ and much higher $$\large K_{\infty}$$. If we assume a $$\large K_{\infty}$$ of 1.3 for instance we get a doubling time of $$\large 2^{-7}$$ seconds, one fifth of a microsecond! After just 10 microseconds power will have increased 10 000 billion times, it is this extraordinary power ramping that allows a bomb to explode, if it was slower the bomb material would tear itself apart long before any decent amount of total energy has been produced.
One group of delayed neutrons
But a reactor with a doubling time of 0.1 seconds would certainly be called a bomb as well (otherwise known as Chernobyl) and I for one wouldn’t go anywhere near it. If that was the end of the story Fermi and his researchers would have died instantly in Chicago when taking pile-1 critical. Obviously that didn’t happen and something slows down reactors, the savior is the aforementioned delayed neutrons. If we make another case where we assume that there is only one group of delayed neutrons and that $$\large\rho$$ is constant we get the equations:
$$\Large \frac{d\phi}{dt} = \frac{\rho-\beta}{\Lambda}k_{\infty}\phi + v\lambda C $$
$$\Large \frac{dC}{dt} = \beta k_{\infty}\Sigma_{a}\phi – \lambda C$$
We can try to assume that the equations have solutions of the form:
$$\large \phi (t) = Ae^{\omega t}$$ $$\large C(t) = Be^{\omega t}$$
If one plugs that proposed solutions into the diffusion and precursor equations and does some algebraic ninjutsu (I won’t bother going through it all here, it’s simple but tedious) one can find a quadratic equation for $$\large\omega$$ with the solutions:
$$\Large \omega_1 = -\frac{k_{\infty}}{2\Lambda}(\frac{\Lambda \lambda}{k_{\infty}} +\beta -\rho) + \sqrt{\frac{k_{\infty}\rho\lambda}{\Lambda} + [\frac{k_{\infty}}{2\Lambda}(\frac{\Lambda\lambda}{k_{\infty}}+\beta -\rho) ]^2}$$
$$\Large \omega_2 = -\frac{k_{\infty}}{2\Lambda}(\frac{\Lambda \lambda}{k_{\infty}} +\beta -\rho) – \sqrt{\frac{k_{\infty}\rho\lambda}{\Lambda} + [\frac{k_{\infty}}{2\Lambda}(\frac{\Lambda\lambda}{k_{\infty}}+\beta -\rho) ]^2}$$
Those are quite messy, lets clean it up a bit by some further approximations. $$\large k_{\infty} $$ is rarely to far away from 1 so lets approximate it away. We can also note that $$\large\lambda\Lambda$$ is much smaller than $$\large\beta-\rho$$ unless $$\large\rho$$ is very close to beta. After rearranging a bit we get:
$$\Large \omega_{1,2} \approx -\frac{1}{2\Lambda}(\beta-\rho) \pm \frac{1}{2\Lambda}\sqrt{ 4\rho\lambda\Lambda+[\beta-\rho]^2}$$
If we rearrange a bit more we can rewrite the above as:
$$\Large\omega_{1,2}\approx-\frac{1}{2\Lambda}(\beta-\rho) \pm\frac{\beta-\rho}{2\Lambda} \sqrt{\frac{4\rho\lambda\Lambda}{(\beta-\rho)^2}+1 }$$
The square root is pretty close to one and we can do a Taylor expansion of it and get rid of all terms with order higher than 1. Then we end up with these two constants:
$$\Large\omega_1 \approx \frac{\rho\lambda}{\beta-\rho}$$
$$\Large\omega_2\approx-\frac{\beta-\rho}{\Lambda}-\frac{\rho\lambda}{\beta-\rho}\approx-\frac{\beta-\lambda}{\Lambda}$$ The point kinetics equation will then become a linear combination of the two solutions:
$$\Large \phi(t) = A_1e^{\frac{\rho\lambda}{\beta-\rho}t}+A_2e^{-\frac{\beta-\rho}{\Lambda}t}$$
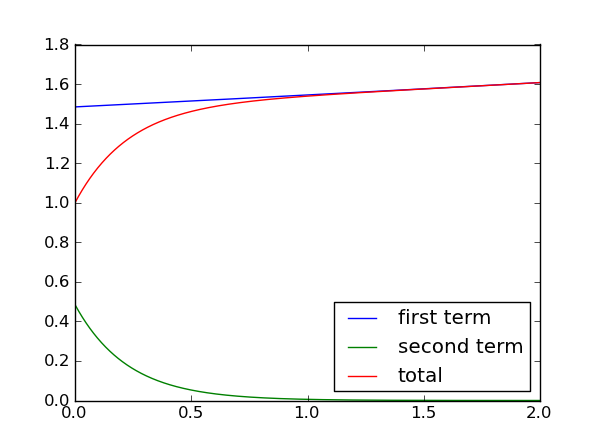
The solution looks like this with the values $$\large\beta=0.0065$$,$$\large\rho=0.0022$$,$$\large\lambda=0.08$$
We see that the second term shrinks rapidly with time if $$\large\rho<\beta$$ and the first term will after a while alone determine the time behavior. We can again calculate the doubling time:
$$\Large T = 0.693\frac{\beta-\rho}{\rho\lambda} $$
If we plug in the same values as above we get a doubling time of about 14 seconds. That is hundred times longer than the doubling time we had in the earlier case without delayed neutrons. Plenty of time for operators or automatic systems to step in and halt any kind of power excursion. This is then the first answer to why a nuclear reactor don’t go kaboom like a bomb. A reactor is operated in a region where delayed neutrons dominates the doubling time. However it is possible to add enough reactivity to a reactor to override the delayed neutrons and make the reactor prompt critical. This happens if the reactivity, $$\rho$$ exceeds the value of delayed neutrons, $$\beta$$. Why doesn’t the reactor blow up in such an event?
It is because in a real reactor reactivity, $$\large\rho$$, is not constant but it changes based on what happens in the reactor. Increase the fuel temperature for instance and reactivity will go up or down. Correctly used this means any deviation from zero reactivity can cancel itself out quickly and that will be the topic of the next blog post.
/Johan